Omer Kajami, poeti që e bëri matematikën të rimonte

Feb 26, 2016 Zani i Nalte Studime 0

nga Redi Shehu

Shumë prej nesh, kur bëhet fjalë për Omer Kajamin (1044-1123), menjëherë biem pre’ e asociimit tradicional të emrit të tij me poezinë dhe mundësisht me Rubairat e famshme, por, në fakt, ekzistenca e personalitetit të tij në historinë dhe kulturën e Orientit dhe Perëndimit lidhet mbi të gjitha me të qenët e tij shkencëtar, matematikan e astronom i spikatur. Kështu kontributi i tij në epokat dhe rrymat kulturore i kalon caqet e njohura të poezisë dhe shtrihet në një oqean dijeje e kontributesh të pazëvendësueshme në këto fusha, duke u bërë një ndër kolosët e mëdhenj që i qëndroi kohërave.

Figura 1

Ajo që njihet si lëvizja e tij e rëndësishme është shkuarja na qytetin e Isfahanit në fillimet e shekullit të 11-të, për të ndërtuar një observator, i cili ishte nën patronazhin e sulltanit selxhuk të asaj kohe Malikshah. Është pikërisht me anën e këtij observatori që Kajami realizoi jo vetëm kalendarin e ashtuquajtur “Kalendari Maliki”, i cili përdorej për mbledhjen e të ardhurave financiare dhe për punë të tjera administrative, por edhe në hartimin të ndoshta katalogut më të madh e të rëndësishëm astronomik, të cilit fatkeqësisht i gjenden vetëm pjesë të vogla të mbetura të tij.[1] Kalendari i Kajamit është konsideruar si kalendar me epërsi të shumta krahasuar me atë Gregorian. Ai, duke i kushtuar vëmendje saktësisë, arriti që në bazë të matjeve të tija të përcaktonte kalendarin diellor me 365.24219858156 ditë. Duke e krahasuar me kalendarin vjetor të ditëve të sotme, i cili është 365.2421190 ditë, shohim që diferenca nga kalendari i hartuar nga Omer Kajami qëndron në disa decimal.[2]

Figura 2

Një ilustrim nga libri i Al Birunit (lindur në shtator të 973) në të cilin tregohen fazat e ndryshme të hënës

Kontributet e Kajamit në shkencën e Algjebrës janë domethënëse. Në librin e tij “Makalat fi al-Xhebr ue al-Mukabila” klasifikoi shume ekuacione algjebrike duke identifikuar 13 forma të ndryshme të ekuacioneve kubike. Ai ishte i pari që arriti të gjente teoremën e binomeve. Ai shkroi një traktat të titulluar “Problemet e Aritmetikës”, duke zhvilluar konceptin e rrënjës së n-së. Ai pohon se metodat e rrënjës katrore dhe të kubit, vijnë nga India, por ai i shtriu ato duke përfshirë të gjitha rendet matematikore përmes metodash pastërtish aritmetike. Kështu Kajami mund të konsiderohet si babai i teoremës binom: (a + b)ⁿ = aⁿ + naⁿ⁻¹b + … + bⁿ e cila u bë baza në zbulimet e rëndësishme të mëvonshme në Islam.[3]

Figura 3: Shënime të Omar Kajamit mbi ndërthurjen e seksioneve konike[4]

Figura 4

Libri “Makalat fi al-Xhebr ue al-Mukabila”, botim i cili klasifikoi shumë ekuacione algjebrike. Mbahet si qasja gjeometrike e Kajamit në zgjidhjen e ekuacioneve

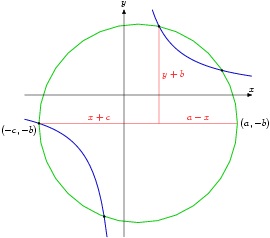
Pasioni i Kajamit për shkencat ekzakte nuk ndalet këtu. Ai është edhe zgjidhësi i ekuacioneve kubike përmes ekuacionit: x³ + 200x = 20x² + 2000. Me anë të përdorimit të numrave në ekuacion, ai përcaktoi trajektoret ndërthurëse të dy seksioneve konike (një rreth dhe një hiperbolë) dhe tregoi se zgjidhja x është e barabartë me gjatësinë e një pjesëze të linjës në diagramë. Në fakt, paraardhësit e tij Al-Hauarizmi në shekullin e 9-të si dhe Thabit Ibn Kurra (836-901), kishin arritur të zgjidhnin ekuacionet katrore duke përdorur elementet e Euklidit. Mirëpo, në atë kohë nuk ishin zbuluar akoma numrat negativë, për rrjedhojë kishin ngelur 14 tipe ekuacionesh të pazgjidhura. Në librin e tij “Traktat i Demonstrimit të Problemeve Algjebrike”, Omar Kajami merret në mënyrë sistematike me të katërmbëdhjetë ekuacionet kubike. Ai arrin të zgjidhë secilin prej tyre duke përdorur seksionet konikë.

Figura 5

Zgjidhja e ekuacioneve kubike sipas Kajamit

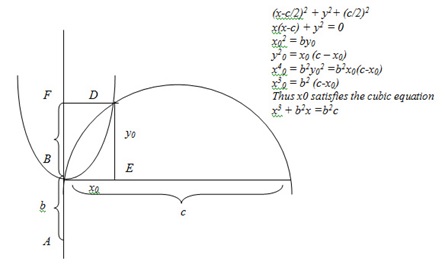
Figura 6

Zgjidhja sipas Kajamit e ekuacioneve të pazgjidhura (x3+qx=r e modifikon në x3 + b2x = b2c)

Në veprën e tij “Shpjegime të Vështirësive në Postulatet e Euklidit”, Kajami merret me postulatet paralele të përcaktimit të raporteve të drejta. Ai rikonstruktoi teorinë e Euklidit duke mos u përpjekur për të provuar postulatet paralele, ai i zëvendësoi ato me dy pohime ku dy vija që nuk puqen duhet të ndërpriten dhe dy vija që puqen nuk mundet kurrë të ndërpriten në drejtimin e puqjes. Ai beson se kjo qasje e tij është një qasje përmirësuese krahasuar me atë të Ibn al-Hejthemit, sepse metodologjia e përdorur nga ky i fundit mbështetej në konceptin e lëvizjes, e cila duhet përjashtuar në rastin e gjeometrisë, sepse Kajami i bashkëngjiste lëvizjen botës materiale dhe e shkëpuste atë nga bota jomateriale e përkuptueshme e gjeometrisë.

Me këtë ai arriti të pasuronte boshllëqet e teoremave të Euklidit. Gjithashtu në studimet e tija për postulatin e pestë, ai u fokusua gjerësisht në konceptin e hapësirës dhe rendit gjeometrik, baza këto të rëndësishme për filozofinë e matematikës. Ndërkohë që Nasirudin al –Tusi e aprovoi teorinë e Kajamit teksa një shekull më vonë zhvilloi më tej teoritë e tij. Po ashtu, Kajami në sajë të punimeve të tija në dy fushat si të algjebrës dhe gjeometrisë, si dhe ndërthurjes që i bëri të dy lëmenjve, mbahet edhe sot si personi i cili arriti të gjeometrizojë algjebrën.

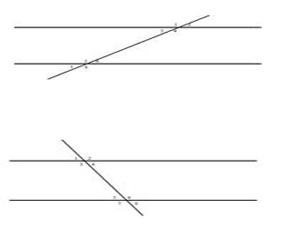
Figura 7

Teoria e linjave paralele

Figura 8

(Nasirudin al Tusi 1274) Faqe të punimeve të tija në arabisht mbi gjeometrinë duke komentuar elementet e Euklidit bazuar në teorinë e Kajamit[5]

Një pikë interesante në të cilën ia vlen të ndalesh, është edhe dallimi që Kajami bëri në studimet e tija, bazuar edhe nga trashëgimia e Ibn Sinës, të trupëzimit natyror dhe trupëzimit matematikor. I pari është botë substanciale e cila qëndron në vetvete, ndërsa trupëzimi matematikor i titulluar edhe volum, futet në kategorinë e pasojave të ardhura si aksident dhe të cilat nuk përbëjnë në vetvete substancë të pavarur. I pari i përket shkencës së natyrës me të cilën ajo rreket të shpjegojë gjërat, ndërsa koncepti i dytë është domethënie e cila lidhet me matematikën. Pikërisht për këtë arsye të ndarjes konceptuale mes këtyre dy disiplinave, Kajami arriti të respektonte këtë ndarje gjatë gjithë punimeve të tija. Ai pikërisht për këtë arsye kritikoi teorinë e Ibn Hejthemit, i cili e kishte përfshirë lëvizjen në kategorinë gjeometrike. Kajami argumenton se lëvizja është kategori e cila i përket trupëzimit natyror dhe nuk duhej futur në disiplinën e gjeometrisë e cila i përket trupëzimit matematikor.

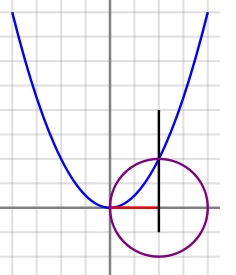
Figura 9

Zgjidhja gjeometrike që Kajami i bëri ekuacioneve kubike

Ky dallim thelbësor i Kajamit u pasua nga El-Tusi më vonë duke hedhur themelet e mekanikës kuantike. Sot për shembull, ka një perceptim për sa i përket elektroneve dhe protoneve si përbërës të trupëzuar, ngjashëm me trupa të tjerë të një shkallë minimale. Por, këto dy kategori i përkasin dy natyrave të ndryshme ekzistenciale. Këtë e përmend edhe Wolfgang Smith në veprën e tij “The Quantum Enigma”, i cili i ndan këto dy kategori në konceptuale dhe trupore.[6] Ky dallim është bazuar në ndarjen konceptuale të Kajamit në filozofinë e matematikës mbi trupëzimet e ndryshme.

Është interesant fakti se ajo që njihet që nga shekulli i 17-të si Trekëndëshi i Paskalit, bazuar në teorinë e matematikanit francez Blaise Pascal, është përpunuar dhe përshkruar nga Omer Kajami i cili së bashku me matematikanin indian Halaudha, njihen si hartuesit e këtij trekëndëshi[7]

Figura 10

Trekëndëshi i përshkruar së pari nga Kajami

Kajami ishte gjithashtu ai që arriti të provonte domethënien gjeometrike të A/C = (A/B) (B/C), e cila përdorej në elementet e Euklidit, por nuk ishte provuar kurrë më parë teorikisht. Kajami arriti të ndërtonte një magnitudë fikse e cila i shërbeu si njësi lidhëse me të gjitha magnitudat e tjera të të njëjtit lloj. Me këtë Kajami arriti të bashkonte në një të vetme si numrat ashtu edhe magnitudat gjeometrike brenda të njëjtit sistem. Për Kajamin magnitudat irracionale janë numra në vetvete të cilat përcaktojnë termin “numer real” të cilin neve e përdorim të gatshëm sot. Ky koncept i futur nga ai shënoi edhe ndryshimin e madh mes matematikës së lashtë greke dhe asaj të kohëve të sotme. Gjenialiteti i Kajamit shtrihet përtej këtyre fushave. Ai është edhe hartuesi i metodologjisë së përcaktimit të gravitetit specifik. Trashëgimia e Kajamit në këto fusha arrin në katër libra mbi matematikën, një libër mbi algjebrën, një tjetër mbi gjeometrinë, si dhe tre libra në fushën e fizikës duke shtuar edhe tre librat në fushën e metafizikës.

Në Perëndim bota akademike zbuloi veprat në shkencat ekzakte të Kajamit që në vitin 1880-të, që u pasuan pastaj me botimin dhe hulumtimin e tyre nga qarqet më të rëndësishme akademike të kohës. Ata e krahasuan Omer Kajamin si dhe pikëpamjen dhe punimet e tija, me matematikanët më të mëdhenj që ata njihnin si Johannes Kepler, Gottfries Wilhelm Leibniz dhe Isak Njuton. Kjo trashëgimi më pas u përmblodh në artikulimin akademik të Perëndimit që në këtë fushë njihet si “Omeriada”.

Karakteristikë e Kajamit në qasjen e tij ndaj shkencave ekzakte, është përpjekja për t’i dhënë shpirt atyre. Ndoshta mund të përbëjë një rast të rrallë që një poet e filozof i një dimensioni të tillë, të arrijë të ruajë staturën e tij edhe në lëmenj të komplikuar siç janë matematika, algjebra, gjeometria dhe fizika. Në përgjithësi letërsia dhe matematika janë konsideruar dhe kanë qëndruar në një distancë të konsiderueshme nga njëra-tjetra për vetë natyrën e tyre tejet të kundërt. Prania e Kajamit në të dy natyrat pa humbur nga asnjëra prej tyre, duke i zhvilluar e ngritur në një nivel akoma më të lartë, përbën edhe një model të asaj që mund të quhet poetizimi i shkencave ekzakte, dhënies shpirt përmes formulimeve filozofike të matematikës e gjeometrisë.

[1]. Moore Patrick, “The Data Book of Astronomy”, Institute of Physics Publishing, Philadelphia 2000 Star Catalogue, f. 327.

[2]. Richards E.G. “Mapping Time: The Calendar and its History” Oxford University Press, 1998, f. 23

[3]. Youschkevitch, Adolphe & Boris Rosenfeld: “Al-Khayyami” In Dictionary of Science Biography. Bot. Charles Gillispie, New York 1973 vol 7, f. 323-334.

[4]. Faqe e parë e dy kapitujve në dorëshkrim të Kajamit, marrë nga Universiteti i Teheranit.

[5]. MS Trinity College Bodleian Library in Oxford.

[6]. Smith Wofgang, “The Quantum Enigma, Peru (Ill.), Sherwood Snyder, viti 2000.

[7]. www.hotmath.com/hotmath_help/topics/yang-huis-triangle.html vizituar 04.06.2012.